【高杆灯生产制作】高杆灯风载荷如何设计与计算

　　高杆灯是指灯杆高度等于或大于20m，作为城市道路和公路、广场、体育场、机场、港口码头等大面积照明的高杆照明设施。高杆灯属于高耸结构，因此，高杆灯的载荷设计就要符合高耸结构的载荷设计要求。高耸结构上的载荷可分为下列三类。

　　(1)永久载荷：结构自重、固定的设备重、物料重、土重、土压力、线的拉力等。

　　喝了西北的烈酒，嚼过关中的馍，再听那高亢的秦腔，便觉得这种说法有几分道理。甘肃许多地方也盛行秦腔，我们一路上也听过不少，但在西安听秦腔，感觉格外地大气苍凉。不知是不是因为千年古都独具悲怆历史，而个体生命面对厚重历史更多的是茫然且无奈，唯有将其投射到秦腔，才好表述那语言难以表达的洞彻历史的穿透力。

　　(2)可变载荷：风载荷、裹冰载荷、常见地震作用、雪载荷、安装检修载荷、塔楼楼面或平台的活载荷、温度变化、地基沉陷等。

　　(3)偶然载荷：导线断裂、索线断线，撞击、爆炸、罕遇地震作用等。

　　说真的，一个品牌的成功，因素肯定是多方面的，从品质到坚持，从外部环境到历史的机遇，从优秀的团队到强大的执行力，从策略到战略……如果作为一个商业案例来分析，没有个几十页，根本无法稍微深入点讲清楚。但有时候，一些细节和侧面也可见一斑。

　　雪荷载为施加在建筑屋面或其他结构外露面上的积雪重量。雪荷载值S由地面积雪重量即基本雪压So乘以屋面积雪分布系数μr确定：

　　S=μrSo [3]

　　基本雪压一般参照规范或者当地气象记录资料。规范给出我国部分大中城市地区10年、50年、100年基本雪压。一般结构取50年基本雪压，临时性建筑、仓储、不重要构筑物等，可按10年、30年取值，或适当调整。

　　影响结构雪载荷大小的主要因素是当地的地面积雪自重和结构件上的积雪分布，他们直接关系到雪载荷的取值和结构安全。

　　裹冰荷载指包围在塔架杆件、缆索、电线表面上的结冰重量。在冬季或早春季节，处于特定气候条件下，在一些地区由冻雨、 冻毛雨、气温低于0℃的雾、云或溶雪冻结形成，其值可根据裹冰厚度和裹冰容重确定。

　　裹冰荷载对于如输电塔架、线路等结构往往是一种重要荷载。由于裹冰增大了杆件、缆索的截面，或封闭了某些格构的空隙，不但使结构或构件的重量增大，而且由于结构挡风面积增大，显著地加大了风荷载，使结构受力更为不利。

　　在此次选取的样本孕妇当中，均进行了三维超声与二维超声检查，使用的探头频率为2.0～5.0MHz，患者需要保持仰卧位进行检查。在进行检查的时候，首先需要对患者的全貌进行检查，同时进行相关数据的收集，对胎儿的颜面部进行仔细的观察，然后对胎儿的具体位置进行分析，进行探头角度的调整，如果显示不太清晰，需要进行适当的加压观察[3]。在形成三维超声以及二维超声成像之后，需要由专门的医生进行判断。

　　地震载荷对高耸结构的破坏是非常严重的，而且该破坏往往还隐藏着潜在危险。

　　地震理论主要包括以下三个。

　　(1)静力理论。该理论不考虑建筑物的动力特性，假设结构物为绝对刚性，地震时建筑物运动与地面运动绝对一致，建筑物的最大加速度等于地面运动的最大加速度，建筑物所受的最大载荷等于其质量与地面最大加速度的乘积。该理论只适用于低矮的，刚性较大的建筑物。

　　(2)反应谱理论。它既考虑了地震时地面的动力特性，也考虑了结构自身的动力特性，是当前工程设计应用最为广泛的地震设计方法之一。反应谱理论是以单质点体系在实际地震作用下的反应为基础来分析结构反应的方法。抗震设计中通常只需地震作用下的最大载荷值，其值为：

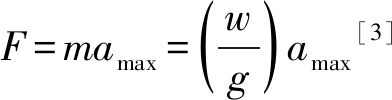
　　式中，w为质点质量，称为水平地震影响因素。

　　(3)直接动力分析理论。反应谱在分析大跨度的柔性结构时，由于非线性因素的影响，反应谱方法的计算误差较大。直接动力分析理论可以克服反应谱理论的缺点。可直接获得地震过程中结构节点各时刻位移，速度，加速度，从而计算各时刻竖向地震作用和构件的地震内力，这些理论称为直接动力分析理论。

　　温度作用应考虑气温变化、太阳辐射及使用热源等因素。作用在结构或构件上的温度作用应采用其温度的变化来表示。计算结构或构件的温度作用效应时，应采用材料的线性热膨胀系数。对于大型或超大型，由不同材料部件组成的结构件，应同时考虑不同部件材料之间的温度作用和整个结构件温度场的变化。

　　作为结构可变载荷之一，温度作用应根据结构施工和使用期间可能同时出现的情况考虑其与其他可变载荷的组合。

　　由于在实际应用当中发现，风载荷是影响高杆灯强度的最大的也是最关键的因素，因此，我们就以40m高杆灯为例，对高杆灯进行风载荷的设计计算。

　　高杆灯的风载荷在各个不同高度处均不同，因此，为了简便起见，我们可以将高杆灯的每一节视为一个质量单元，共分为五个质量单元。对这些质量单元进行风载荷的计算(即计算F0、F1、F2、F3、F4)，就可以近似得到整个高杆灯的风载荷。高杆灯的载荷计算模型见图3。

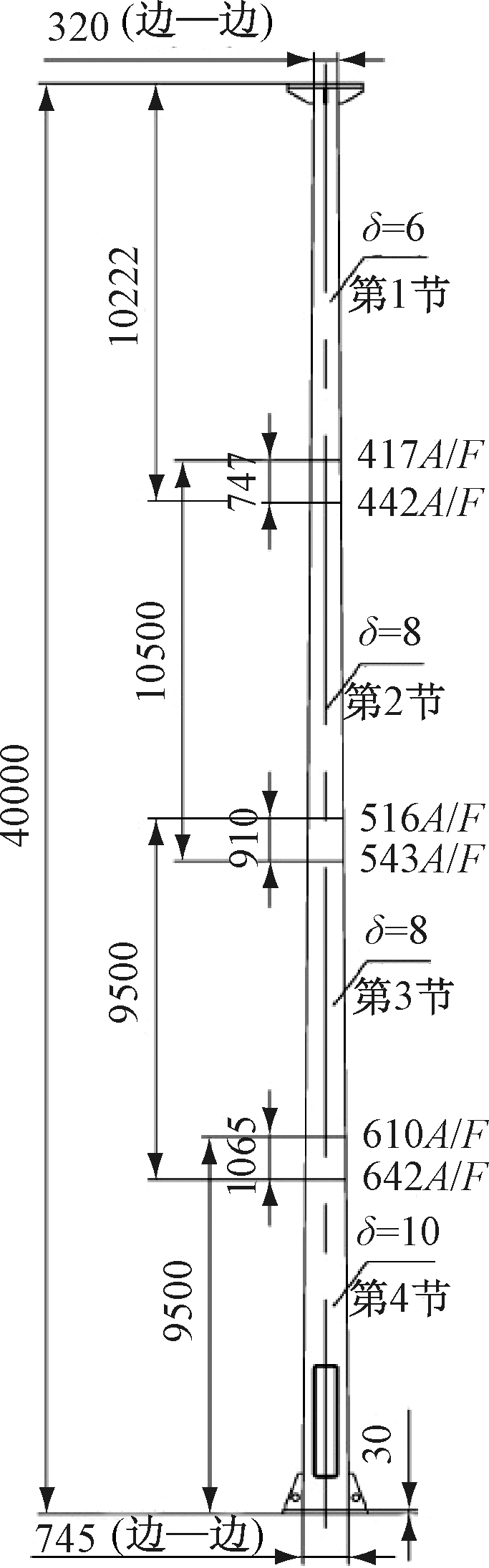
　　图3 高杆灯尺寸图

　　Fig.3 Dimemtions of mast

　　作用在高杆灯上单位面积上的风载荷应按照下式计算：

　　ωh=βzμsμzμrωo[2]

　　式中，ωh为用在高杆灯单位面积上的风载荷(单位：kN/m2);ωo为基本风压(单位：kN/m2);μr为重现期调整系数，对一般高耸结构可采用1.1，对重要高耸结构可采用1.2;μz为z高度处的风压高度变化系数;μs为风载荷体型系数，对高杆灯选取0.7;βz为z高度处的风振系数。